During my studies I worked on several different research areas, seemingly unrelated to each other. What combines them are their aspects of intricate dynamical behavior, critical transitions or novel phenomena based on entanglement. In the following I’ll give a short overview over the main projects.
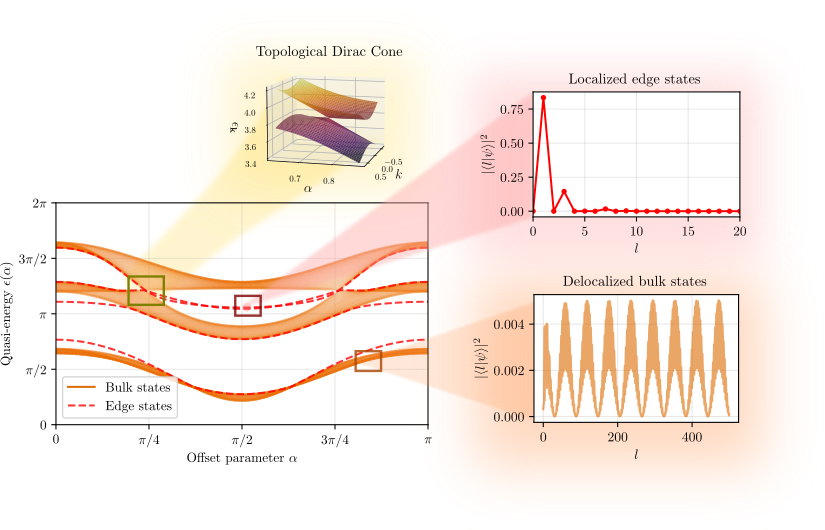
Topological phases with periodically kicked molecules
In this work with Misha Lemeshko we engineered topological charges using molecules which are driven by periodic laser pulses. The angular momentum lattice allows to map systems from condensed matter physics to this AMO system and study their real-time behavior. We discover topological Dirac cones, protected by time-reversal and inversion symmetry. Finally, we provide experimental signatures of the topological behavior which boil down to experimentally feasible observables like the alignment or orientation of the molecule.
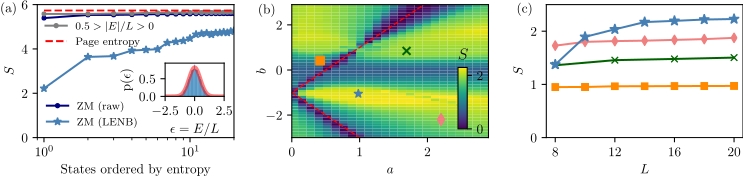
Area-Law Entangled Eigenstates from Nullspaces
This project came out of a rotation with the Group of Serbyn Maksym. A Hamiltonian with two symmetries that anti-commute which each other exhibits an extensive degenerate subspace, in our case with zero energy. We consider such Hamiltonians with local interactions and determine the state with the lowest entropy within the zero-energy subspace. Surprisingly, the entropy of these states scale with area-law. We underline our hypothesis with exact diagonalization studies. For special points like the PxP model we recover the “Quantum scar” states already found in previous studies.
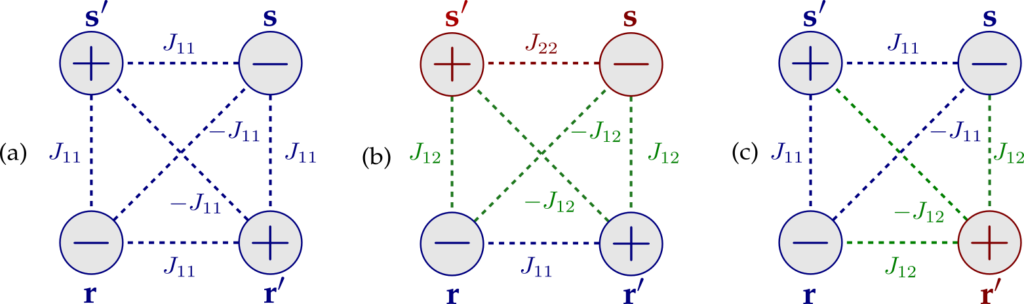
Break-down of Superfluidiy in 2D Bose mixtures
In my Maser Thesis (under supervision of Tilman Enss) I analyzed the phase diagram of a binary Bose mixture in two dimensions at low temperatures. Similar to a single Bose gas, where the BKT transition from superfluid to normal phase can be observed, we investigate what happens when topological vortices of the different species diminish the superfluid density. Since the Bose mixture is interacting, the vortices are interacting as well and form composite vortex pairs (reminiscent of the so-called Counter/ Coflow of a binary mixture). Finally, we establish the RG flow and determine the new critical temperature. We find that the break-down of one superfluid can induce the other superfluid to break-down as well.
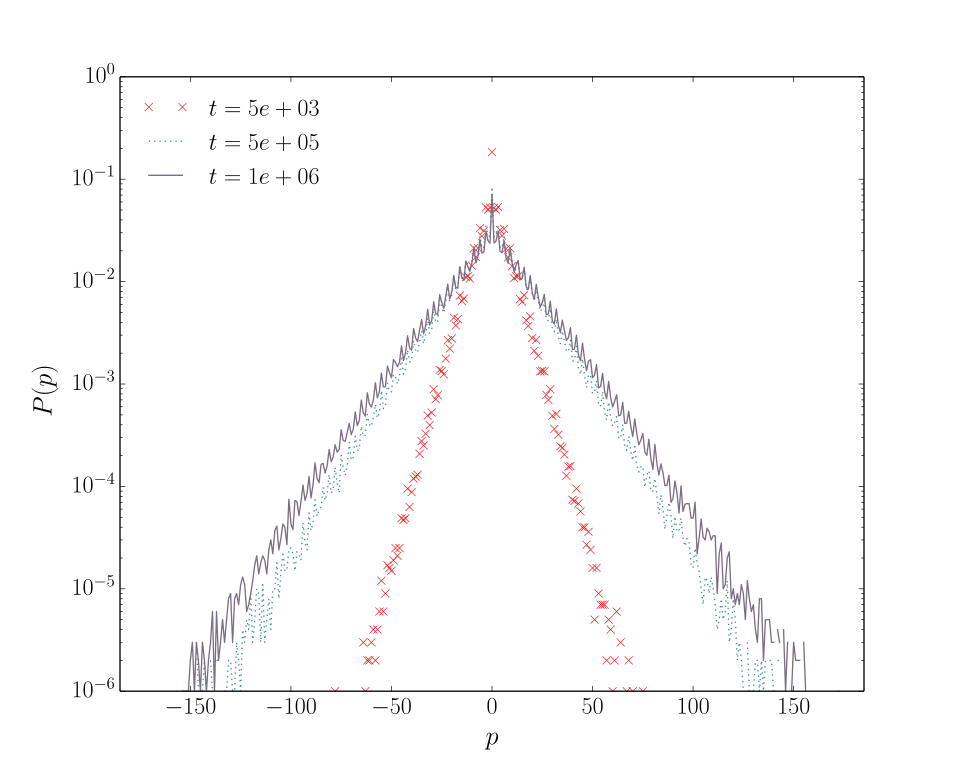
Classical Dynamical localization
A periodically kicked rotor can display behavior which is very different from its semi-classical counterpart, framed dynamical localization (which is also related to Quantum Chaos). As it turns out, the main ingredient of this phenomenon is that in Quantum mechanics the phase space is discretized in units of hbar. We tried what happens when we consider a classical system with discrete phase space structure and we discovered a similar localization phenomenon.